Benjamin J. Zhang

Benjamin J. Zhang

Postdoctoral Research Associate @ UNC Chapel Hill School of Data Science and Society

Research

Research Overview

I am an applied and computational mathematician with research interests in establishing the mathematical foundations of machine learning (ML) methods and their application in scientific computing. My research program offers new frameworks for understanding ML methods through established mathematical disciplines, enhancing and innovating methods based on those insights, and principled application to scientific computing problems.

My recent work focuses on generative artificial intelligence (AI) through the lens of partial differential equations (PDEs) arising from mathematical control theory and optimal transport. This perspective extends from deep learning architectures to scientific computing applications, leading to methodological improvements and analysis that yield a deeper understanding of state-of-the-art generative flow algorithms. Simultaneously, my study of generative AI produces algorithms for trustworthy scientific machine learning. In particular, my work on robust generative modeling for random differential equations enables probabilistic foundations for operator learning, grounding foundation models for differential equations in this framework and providing uncertainty quantification (UQ). UQ is a recurring theme in my research program, which provides tools for obtaining statistical guarantees, understanding stability of algorithms, and confidence in generative algorithms.

Research Tree

Principled generative AI rooted in mathematical foundations enables improved theory-informed models and trustworthy application in scientific computing.

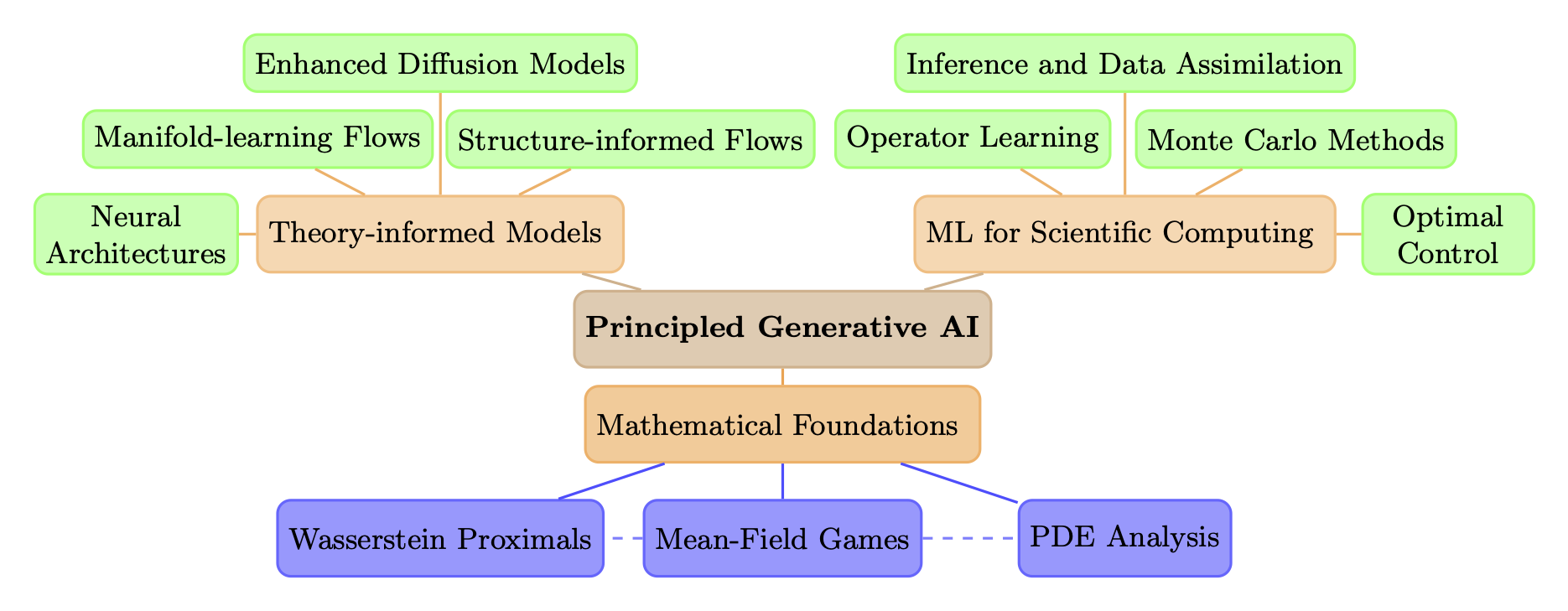
Research Tree

Principled Generative AI Mathematical Foundations Mean-Field Games Wasserstein Proximals PDE Analysis Neural Architectures Theory-informed Models Manifold-learning Flows Structure-informed Flows Enhanced Diffusion Models Scientific ML Operator Learning Monte Carlo Methods Optimal Control

Research Themes

Mathematical Principles of Generative AI: Foundations and Analysis

State-of-the-art generative models learn to evolve samples from a simple reference to complex target distributions through differential equations trained on finite example datasets (e.g., images, molecules). Understanding their mathematical foundations is critical for reliable downstream scientific applications. In my work A mean-field games laboratory for generative modeling, I show how mean-field games (MFGs) provide foundational mathematical principles for major classes of generative flows through PDEs. This mathematical foundation enables PDE-based analysis, yielding insights on data efficiency, training behavior, and approximation guarantees. My recent work on Wasserstein proximal operators reveals a deeper principle: robust generative flows compute so-called proximal optimal transport divergences — measures of discrepancy between probability distributions that interpolate between classical divergences and transport distances. The MFG provides a computable instantiation of this broader framework.

Related publications:

  • • N. Mimikos-Stamatopoulos, B.J. Zhang, and M.A. Katsoulakis. "Score-based generative models are provably robust: an uncertainty quantification perspective." NeurIPS 2024. [arXiv:2405.15754]
  • • K. Kan, X. Li, B.J. Zhang, T. Sahai, S.J. Osher, and M.A. Katsoulakis. "Optimal Control for Transformer Architectures: Enhancing Generalization, Robustness and Efficiency." NeurIPS 2025. [arXiv:2505.13499]
  • • B.J. Zhang and M.A. Katsoulakis. "A mean-field games laboratory for generative modeling." 2023. [arXiv:2304.13534]
  • • Z. Chen, M.A. Katsoulakis, and B.J. Zhang. "Equivariant score-based generative models provably learn distributions with symmetries efficiently." 2024. [arXiv:2410.01244]
  • • R. Baptista, P. Birmpa, M.A. Katsoulakis, L. Rey-Bellet, and B.J. Zhang. "Proximal optimal transport divergences." 2025. [arXiv:2505.12097]

Mathematically-Informed Generative Modeling Methodology

The analyses provided by mean-field games, optimal transport, and information theory reveal mathematical structure which I have used to develop new mathematically-informed generative flows. These flows can be trained faster, more robustly, and with less data. My work demonstrates that well-posed formulations lead to robust generative models for learning distributions on low-dimensional manifolds, overcoming issues in training stability that arise from low-dimensional data and choices in model parametrization. Additionally, I have developed structure-preserving generative models that incorporate symmetries and prior knowledge, which enable more efficient learning of structured distributions. This theory-driven approach shows how understanding mathematical principles translates to practical improvements in generative modeling performance.

Related publications:

  • • J. Birrell, M.A. Katsoulakis, L. Rey-Bellet, B.J. Zhang, and W. Zhu. "Nonlinear denoising score matching for enhanced learning of structured distributions." Computer Methods in Applied Mechanics and Engineering 2025. [arXiv:2405.15625]
  • • H. Gu, M.A. Katsoulakis, L. Rey-Bellet, and B.J. Zhang. "Combining Wasserstein-1 and Wasserstein-2 proximals: robust manifold learning via well-posed generative flows." 2024. [arXiv:2407.11901]
  • • B.J. Zhang, S. Liu, W. Li, M.A. Katsoulakis, and S.J. Osher. "Wasserstein proximal operators describe score-based generative models and resolve memorization." 2024. [arXiv:2402.06162]

Principled Generative Approaches to Scientific Machine Learning

My mathematically principled generative approaches enable new solutions to problems in scientific computing. One recent focus is a generative perspective for operator learning. Operator learning involves training statistical models to approximate solution operators of ordinary and partial differential equations, forming the basis for their foundation models. A major gap in ML-based operator learning methods is their lack of trustworthiness compared to traditional model-order reduction methods. My research addresses this by establishing a probabilistic framework for operator learning that provides uncertainty quantification for these methods. Additionally, I use connections between generative AI and control theory to address the curse of dimensionality in high-dimensional scientific computing problems, developing generative approaches for rare event simulation, sampling methods for Bayesian inference, and optimal control.

Related publications:

  • • B.J. Zhang, Y.M. Marzouk, and K. Spiliopoulos. "Transport map unadjusted Langevin algorithms: Learning and discretizing perturbed samplers." Foundations of Data Science 2025. [arXiv:2302.07227]
  • • B.J. Zhang, T. Sahai, and Y.M. Marzouk. "A Koopman framework for rare event simulation in stochastic differential equations." Journal of Computational Physics 2022. [arXiv:2101.07330]
  • • B.J. Zhang, Y.M. Marzouk, and K. Spiliopoulos. "Geometry-informed irreversible perturbations for accelerated convergence of Langevin dynamics." Statistics and Computing 2022. [arXiv:2108.08247]
  • • B.J. Zhang, T. Sahai, and Y. Marzouk. "Sampling via controlled stochastic dynamical systems." NeurIPS Workshop 2021.
  • • B.J. Zhang, S. Liu, S.J. Osher, and M.A. Katsoulakis. "Probabilistic operator learning: generative modeling and uncertainty quantification for foundation models of differential equations." 2025. [arXiv:2509.05186]
  • • P. Dupuis and B.J. Zhang. "Particle exchange Monte Carlo methods for eigenfunction and related nonlinear problems." 2025. [arXiv:2505.23456]

For a complete list of my publications, please visit my Publications page.